【自由への一歩】貯蓄率と投資リターン（運用率）による、「仕事をしなくても生きていける財源」への達成までの時間について
貯蓄率と投資リターン（運用率）による、「仕事をしなくても生きていける財源」への達成までの時間について記載します。
前回のおさらい
-------------
私自身の節約に対する考えをまとめた。
まとめ回だったので、内容は割愛させていただきます。
-------------
『貯蓄率と投資リターン（運用率）による、「仕事をしなくても生きていける財源」への達成までの時間』
今回は、「長期的な予算のたて方」の記事で、ご紹介した
『貯蓄率と投資リターン（運用率）による、「仕事をしなくても生きていける財源」への達成までの時間』
に関して、計算方法を記載したいと思います。
計算方法
-------------
a：１年間の手取り収入
b：１年間の貯蓄率（%）
c：１年間の運用率（年利）（％）
n：「仕事をしなくても生きていける財源」への達成までの時間
※１：仕事をしなくても生きていける財源 ＝ １年間の支出×25倍（円）とする。
※２：「仕事をしなくても生きていける財源」への達成までの時間については、資産が０円からスタートした場合の期間となる。
上記の条件の場合、下記の式で算出できる。
（ （ 100 + c ）/ 100 ）^n ≧ （ （ c ×（100-b） ）+4b）/ 4b
→ b：１年間の貯蓄率（％） と c：１年間の運用率（年利）（％）を設定できれば、
n：「仕事をしなくても生きていける財源」への達成までの時間を算出できる。
-------------
上記、結論のとおり計算すると、n：「仕事をしなくても生きていける財源」への達成までの時間を算出できます。
なお、※１：仕事をしなくても生きていける財源 ＝ １年間の支出×25倍（円）について、
２５倍としている理由は、年利４％で運用（投資）したときに、運用（投資）により１年間の支出を支払うことができる財源だからです。
つまり、仕事をしなくても、運用益により支出を払える状態となるための数字が、２５倍ということです。
今回の記事は、
（ （ 100 + c ）/ 100 ）^n ≧ （ （ c ×（100-b） ）+4b）/ 4b
をどのようにして導いたかを説明します。
具体例を用いて算出
いきなり上記のように文字式を使用して説明すると、ややこしいので、下記の具体例を用いて説明します。
-------------
１年間の手取り：５００万円
１年間の支出 ：４００万円
１年間の貯蓄 ：１００万円 （貯蓄率２０％）
運用率 ：１００万円積立 年利４％
の場合、４２年後に仕事をしなくても生きていける財源となる。
-------------
上記の条件の場合、下記のように増えていきます。
０年目：０円
１年目：１００万円
２年目：１００万円 × 1.04 ＋１００万円
３年目：１００万円 × 1.04^2 ＋ １００万円 × 1.04 ＋ １００万円
k年目：１００万円 × 1.04^（k-1） ＋ １００万円 × 1.04^(k-2) ＋ ・・・ ＋１００万円
となります。
k年目について、項の順番を入れ替えると、下記のようになります。
k年目：１００万円 ＋ ・・・ ＋ １００万円 × 1.04^(k-2) ＋ １００万円 × 1.04^（k-1）
k年目を計算します。
この計算は、高校生の数学で習う数学Bの数列で解けます。
「等比数列の和」となっているのです。
それが、分かれば、下記のように表現することができます。
この値が、「１年間の支出 ：４００万円」 × ２５ 以上になれば良いので、
下記のようになります。
「等比数列の和」は公式があり、下記により算出できます。
上記公式を利用して計算をした結果、下記のようになります。
1.04^n ≧ 5
このnを求めると、最小で４２という数字が出てきます。
nの求め方は、Excelを使用しました。
下記のようなイメージです。
A列 B列 C列
1 1.04 B列の掛け算（=PRODUCT( : )）
2 1.04
3 1.04
4 1.04
5 1.04
・
・
・
42 1.04
A列が４２で５を上回りました。
つまり、４２年目で仕事をしなくても生きていける財源に到達できるということが分かります。
文字式を用いて算出
-------------
a：１年間の手取り収入（円）
b：１年間の貯蓄率（%）
c：１年間の運用率（年利）（％）
n：「仕事をしなくても生きていける財源」への達成までの時間（年）
上記の条件の場合、下記の式で算出できる。
（ （ 100 + c ）/ 100 ）^n ≧ （ （ c ×（100-b） ）+4b）/ 4b
-------------
上記の条件より
１年間の貯蓄額：a× (b/100) （円）
１年間の支出額：a× (1 - ( b/100 ) ）（円）
となります。
具体例と同様に、０年目からｋ年目の増え方を下記に記載します。
※下記単位は（円）です。
０年目：０
１年目：（a× (b/100) ）
２年目：（a× (b/100) ）×（（100+c）/100）
３年目：（a× (b/100) ）×（（100+c）/100 ）^2 ＋ （a× (b/100) ）×（（100+c）/100） ＋ （a× (b/100) ）
k年目：（a× (b/100) ）×（（100+c）/100 ）^（k-1） ＋ （a× (b/100) ）×（（100+c）/100 ）^(k-2) ＋ ・・・ ＋（a× (b/100) ）
となります。
k年目について、項の順番を入れ替えると、下記のようになります。
k年目：（a× (b/100) ） ＋ ・・・ ＋ （a× (b/100) ）×（（100+c）/100 ）^(k-2) ＋ （a× (b/100) ）×（（100+c）/100 ）^（k-1）
k年目を計算します。
文字式でややこしくなっていますが、具体例と同じ増え方なので、「等比数列の和」です。
下記のように表現できます。
この値が、「１年間の支出額（ a× (1 - ( b/100 ) ） ）」 × ２５ 以上になれば良いので、
下記のようになります。
上記の式を「等比数列の和」の公式を使用して、整理していくと下記となります。
（ （ 100 + c ）/ 100 ）^n ≧ （ （ c ×（100-b） ）+4b）/ 4b
上記の式のnの求め方は、具体例と同様にExcelを使用すると計算できます。
b：１年間の貯蓄率（%）
c：１年間の運用率（年利）（％）
を設定すれば、具体例と同様に値が出てくるので、条件を決めさえすれば算出できます。
A列 B列 C列
1 （ （ 100 + c ）/ 100 ） B列の掛け算（=PRODUCT( : )）
2 （ （ 100 + c ）/ 100 ）
3 （ （ 100 + c ）/ 100 ）
4 （ （ 100 + c ）/ 100 ）
5 （ （ 100 + c ）/ 100 ）
・
・
・
50 （ （ 100 + c ）/ 100 ）
b：１年間の貯蓄率（%）
c：１年間の運用率（年利）（％）
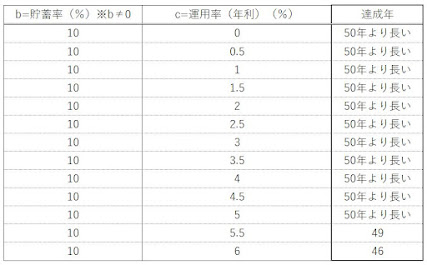
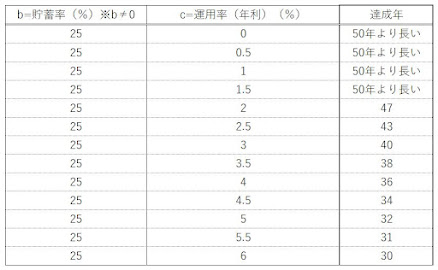
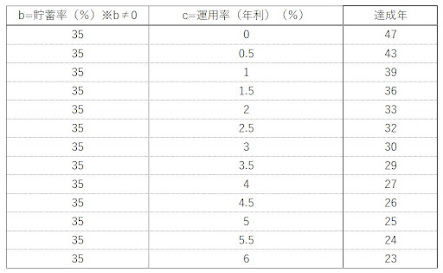
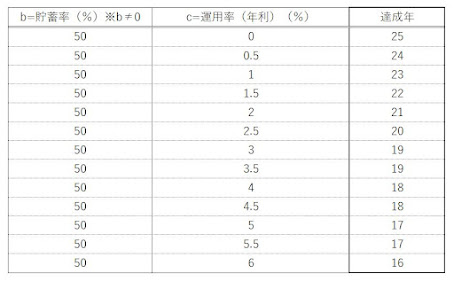
をいろいろなパターンで試算したものが、
「長期的な予算のたて方」の記事で、ご紹介した一覧表となります。
「長期的な予算のたて方」は人生の目標設定に大きく影響するため、自分自身で責任を持って戦略をたてることが大切だと思います。
参考になれば幸いです。
（参考）私が算出した一覧表です。
●貯蓄率５％の場合
●貯蓄率１０％の場合
●貯蓄率１５％の場合
●貯蓄率２０％の場合
●貯蓄率２５％の場合
●貯蓄率３０％の場合
●貯蓄率３５％の場合
●貯蓄率４０％の場合
●貯蓄率４５％の場合
●貯蓄率５０％の場合
今回はここまでです。
ありがとうございました。
0 件のコメント:
コメントを投稿